函数式编程进阶：应用函子

2020-11-06

pipeline & function compose

图片来源: https://unsplash.com/photos/FqYMtQpE77E

本文作者：赵祥涛

上一章中介绍了 Functor(函子) 的概念，简单来说，就是把一个 “value” 填装进 “Box” 中，继而可以使用 map 方法映射变换 Box 中的值：Box(1).map(x => x+1)。本章我们在继续在 Box 的基础上继续扩展其他更强大的理念，从纯函数与副作用的概念及用途作为承上启下的开端，继续巩固 Functor 的概念以及接下来将要介绍的 Applicative Functor 的引子。

函数式编程中纯函数是一个及其重要的概念，甚至可以说是函数组合的基础。你可能已经听过类似的言论：“纯函数是引用透明( Referential Transparency )的”，“纯函数是无副作用( Side Effect )的”，“纯函数没有共享状态( Shared State )”。下面简单介绍下纯函数。

纯函数与副作用

在计算机编程中，假如满足下面这两个条件的约束，一个函数可以被描述为一个“纯函数”( pure function )

给出相同的参数，那么函数的返回值一定相同。该函数结果值不依赖任何隐藏信息或程序执行处理可能改变的状态，也不能依赖于任何来自 I/O 的外部输入。
在对函数返回值的计算过程中，不会产生任何语义上可观察的副作用或输出，例如对象的变化或者输出到 I/O 的操作。

关于纯函数的第一条很简单，相同的输入，总会返回相同的输出，和中学数学中学习的“函数”完全类似，传入相同的参数，返回值一定相同，函数本身就是从集合到集合的“映射”。

第二条不产生可观察的副作用又是什么意思呢？也就是函数不可以和系统的其他部分通信。比如：打印日志，读写文件，数据请求，数据存储等等；

从代码编写者的角度来看，如果一段程序运行之后没有可观察到的作用，那他到底运行了没有？或者运行之后有没有实现代码的目的？有可能它只是浪费了几个 CPU 周期之后就去睡大觉了！

从 JavaScript 语言的诞生之初就不可避免地需要能够与不断变化的，共享的，有状态的 DOM 互相作用；如果无法输入输出任何数据，那么数据库有什么用处呢？如果无法从网络请求信息，我们的页面又该如何展示？没有 “side effect” 我们几乎寸步难行，副作用不可避免，上述的任何一个操作，都会产生副作用，违反了引用透明性，我们似乎陷入了两难的境地！

世間安得雙全法，不負如來不負卿

如何在 keep pure 的前提下，又能妥善的处理 side effect 呢？

惰性盒子-LazyBox

要想较理想的解决这个问题，我们把注意力转回到 JavaScript 的核心 function 上，我们知道在 JavaScript 里，函数是“一等公民”，JavaScript 允许开发人员像操作变量一样操作函数，例如将函数赋值给变量、把函数作为参数传递给其他函数、函数作为另一个函数的返回值，等等...

JavaScript 函数具有值的行为，也就是说，函数就是一个基于输入的且尚未求值的不可变的值，或者可以认为函数本身就是一个等待计算的惰性的值。那么我们完全可以把这个“惰性的值”装入 Box 中，然后延迟调用即可，仿照上一章的 Box ，可以实现一个 Lazy Box ：

const LazyBox = g => ({
    map: f => LazyBox(() => f(g())),
    fold: f => f(g())
})

注意观察，map 函数所做的一直都是在组合函数，函数并没有被实际的调用；而调用 fold 函数才会真正的执行函数调用，看例子：

const finalPrice = str =>
    LazyBox(() => str)
        .map(x => { console.log('str:', str); return x })
        .map(x => x * 2)
        .map(x => x * 0.8)
        .map(x => x - 50)  

const res = finalPrice(100)
console.log(res)  // => { map: [Function: map], fold: [Function: fold] }

在调用 finalPrice 函数的时候，并没有打印出 'str:100'，说明正如我们预期的那样，函数并没有真正的被调用，而只是在不断的进行函数组合。在没有调用 fold 函数之前，我们的代码都是 "pure" 的。

这有点类似于递归，在未满足终止条件之前(没有调用 fold 之前)，递归调用会在栈中不断的堆叠(组合函数)，直到满足终止条件(调用 fold 函数)，才开始真正的函数计算。

const app = finalPrice(100)
const res2 = app.fold(x => x)

console.log(res2) // => 110

fold 函数就像打开潘多拉魔盒的双手；通过 LazyBox 我们把可能会“弄脏双手(产生副作用)”的代码扔给了最后的 fold ，这样做又有什么意义呢？

把代码中不纯的部分剥离出来，保障核心部分代码的 “pure” 特性，比如上面的代码中只有 app.fold(x => x) 是 “no pure” 的，其他部分都是 “pure”
类似于上一章中的错误集中管理，可以通过 LazyBox 来把副作用集中管理，如果在项目中不断的扩大 “pure” 的部分，我们甚至可以把不纯的代码推到代码的边缘，保证核心部分的 “pure” 和 “referential transparency”

LazyBox 也和 Rxjs 中的 Observable 有很多相似之处，两者都是惰性的，在 subscribe 之前，Observable 也不会推送数据。

此处请思考下 React 中的 useEffect 以及 Redux 中的 reducer ，action 分离的设计理念。

应用函子

Function in Box

上一小结，介绍了把函数装入 LazyBox 中，放在最后延迟执行，以保障最后大多数代码的 “pure” 特性。

转换下思维，函数可以认为是“惰性的值”，那么我们把这个稍显特殊的值，装入普通的 Box ，又会发生什么呢？还是从小学数学开始吧。

const Box = x => ({
    map: f => Box(f(x)),
    inspect: () => `Box(${x})`
})

const addOne = x => x + 1
Box(addOne) // => Box(x => x + 1)

inspect 方法的目的是为了使用 Node.js 中的 console.log 隐式的调用它，方便我们查看数据的类型；而这一方法在浏览器中不可行，可以用 console.log(String(x)) 来代替; Node.js V12 API 有变更，可以采用 Symbol.for('nodejs.util.inspect.custom') 替代 inspect

现在我们得到了一个包裹着函数的 Box ，可是我们怎么使用这个函数呢？毕竟 Box(x).map 方法都是接收一个函数！继续回到函数 addOne 上，我们需要一个数字，传递给 addOne ，对吧！所以换句话说就是，我们怎么传递一个数字进去应用这个 addOne 函数呢，答案非常简单，继续传递一个被包裹的值，然后 map 这个函数 (addOne) 不就可以啦! 看代码：

const Box = x => ({
    map: f => Box(f(x)),
    apply: o => o.map(x),
    flod: f => f(x),
    inspect: () => `Box(${x})`
})
Box(addOne).apply(Box(2)) // => Box(3)

看看 Box 神奇的新方法，首先被包裹的值是一个函数 x ，然后我们继续传递另一个 Box(2) 进去，不就可以使用 Box(2) 上的 map 方法调用 addOne 函数了吗！

现在重新审视一下我们 Box(addOne) ，Box(1) ，那么这个问题实际上可以归结为：把一个 functor 应用到另一个上 functor 上，而这也就是 Applicative Functor (应用函子)最擅长的操作了，看一下示意图来描述应用函子的操作流程：

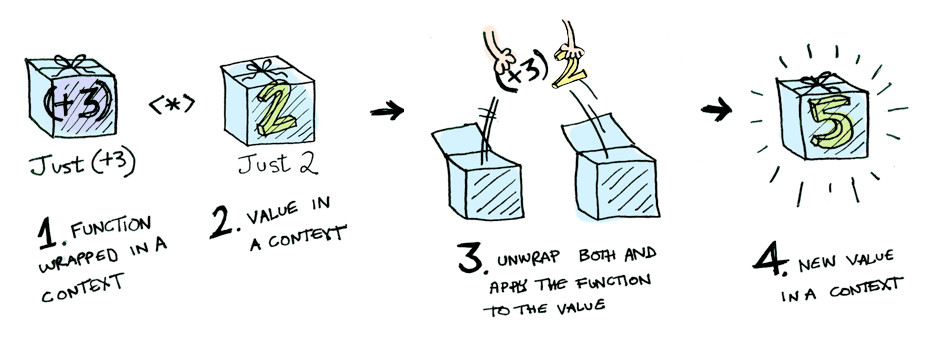
Applicative Functor

所以根据上面的讲解和实例我们可以得出一个结论：先把一个值 x 装进 Box，然后 map 一个函数 f 和把函数 f 装进 Box，然后 apply 一个已经已经装进 Box 的 x，是完全等价的！

F(x).map(f) == F(f).ap(F(x))

Box(2).map(addOne) == Box(addOne).apply(Box(2))  // => Box(3)

根据规范，apply 方法后面我们会简写为ap!

Applicative functor (应用函子) 也是函数式编程中一大堆“故弄玄虚”的概念中唯一的比较“名副其实”的了，想想 Functor(函子)

应用函子与函数柯里化

在继续学习函数柯里化之前，先复习一下中学数学中的高斯消元法：设函数 f(x,y) = x + y，在 y = 1 的时候，函数可以修改为 f(x) = x + 1 。基本思路就是把二元变成一元，同理我们可以把三元函数降元为二元，甚至把多元函数降元为一元函数。

那么我们可以在一定程度上认为函数求值的过程，就是就是函数消元的过程，当所有的元都被消完之后，那么就可以求的函数值。

数学中的高斯消元法和函数式编程中的“柯里化”是有点类似的，所谓函数柯里化就是把一个接收多个参数的函数，转换为一次接收一个参数，直到收到全部参数之后，进行函数调用(计算函数值)，看例子：

const add = (x, y) => x + y
const curriedAdd = x => y => x + y

好了，简单理解了函数柯里化的概念之后，继续往前走一步，思考一下，如果现在有两个「被包裹的值」，怎么把一个函数应用上去呢？举个例子：

const add = x => y => x + y

add(Box(1))(Box(2))

上面的方案明显是走不通的，我们没办法直接把 Box(1) 和 Box(2) 相加，他们都在盒子里;

可是我们的需求不就是把 Box(1) ，Box(2)，add 三者互相应用一下，想要得到最后的结果 Box(3)。

从第一章开始，我们的函数运算都是在 Box 的“保护”下进行的，现在不妨也把 add 函数包装进 Box 中，不就得到了一个应用函子 Box(add)，然后继续 “apply” 其他的函子了吗？

Box(add).ap(Box(1))  // => Box(y => 1 + y) (得到另一个应用函子)
Box(add).ap(Box(1)).ap(Box(2))  // => Box(3) (得到最终的结果)

上面的例子，因为每次 apply 一个 functor ，相当于把函数降元一次，我们可以得出一个结论，一个柯里化的函数，有几个参数，我们就可以 apply 几次。

每次 apply 之后都会返回包裹新函数的应用函子，换句话说就是：应用多个数据到多个函数，这和多重循环非常类似。

应用函子的应用案例

表单校验是我们日常开发中常见的一个需求，举个具体的例子，假如我们有一个用户注册的表单，我们需要校验用户名，密码两个字段，常见的代码如下：

const checkUserInfo = user => {
    const { name, pw, phone } = user
    const errInfo = []
    if (/^[0-9].+$/.test(name)) {
        errInfo.push('用户名不能以数字开头')
    }
    if (pw.length <= 6) {
        errInfo.push('密码长度必须大于6位')
    }

    if (errInfo.length) {
        return errInfo
    }
    return true
}

const userInfo = {
    name: '1Melo',
    pw: '123456'
}

const checkRes = checkUserInfo(userInfo)
console.log(checkRes)  // => [ '用户名不能以数字开头', '密码长度必须大于6位' ]

这个代码自然没有问题，但是，假如我们要继续添加需要校验的字段(e.g.,电话号码，邮箱)， checkUserInfo 函数毫无疑问会越来越庞大，并且如果我们要修改某一个字段的校验规则的话，整个 checkUserInfo 函数可能会受到影响，我们需要增加的单元测试工作要更多了。

回想一下第一章中介绍的 Either(Left or Rigth) Right 指代正常的分支，Left 指代出现异常的分支，他们两者绝不会同时出现，现在我们稍微换个理解方式：Right 指代校验通过的分支，Left 指代校验不通过的分支。

此时我们继续在第一章 Either 的基础上扩展其他的属性和方法，用来做表单校验的工具：

const Right = x => ({
    x,
    map: f => Right(f(x)),
    ap: o => o.isLeft ? o : o.map(x),
    fold: (f, g) => g(x),
    isLeft: false,
    isRight: true,
    inspect: () => `Right(${x})`
})

const Left = x => ({
    x,
    map: f => Left(x),
    ap: o => o.isLeft ? Left(x.concat(o.x)) : Left(x),
    fold: (f, g) => f(x),
    isLeft: true,
    isRight: false,
    inspect: () => `Left(${x})`
})

相对比与原 Either，新增了 x 属性和 ap 方法，其他的属性完全类似，就不做解释了；新增 x 属性的原因在于需要记录表单校验的错误信息，这个很好理解，而新增的 isLeft ，isRight 属性就更简单了，用来区分 Left/Right 分支。

我们仔细看一下新增的 ap 方法，先看 Right 分支的 ap: o => o.isLeft ? o : o.map(x)，毫无疑问 ap 方法接收另一个 functor ，如果另一个 functor 是 Left 的实例，则不需要 Right 处理直接返回，如果是 Right ，则和平常 applicative functor 一样，对 o 作为主体进行 map。

Left 分支上的 ap: o => o.Left ? Left(x.concat(o.x)) : Left(x)，如果是 Left 的实例，则进行一个“叠加”，实际上就是为了累加错误信息，而如果不是 Left 的实例则直接返回原本已经记录的错误信息。

做好了前期的准备工作，我们就可以大刀阔斧的按照函数式的思维(函数组合)来拆分一下 checkUserInfo 函数：

const checkName = name => {
    return /^[0-9].+$/.test(name) ? Left('用户名不能以数字开头') : Right(true)
}

const checkPW = pw => {
    return pw.length <= 6 ? Left('密码长度必须大于6位') : Right(true)
}

上面把两个字段校验从一个函数中拆分成了两个函数，更重要的是完全解耦；返回值要么是校验不通过的 Left ，要么是校验通过的 Right ，所以我们可以理解为现在有了两个 Either，只要我们再拥有一个 被包裹进Either盒子并且柯里化两次的函数 不就可以让他们互相 apply 了吗？

const R = require('ramda')

const success = () => true

function checkUserInfo(user) {
    const { name, pw, phone } = user
    // 2 是因为我们需要 `ap` 2 次。
    const returnSuccess = R.curryN(2, success);

    return Right(returnSuccess)
        .ap(checkName(name))
        .ap(checkPW(pw))
}

const checkRes = checkUserInfo({ name: '1Melo', pw: '123456' })
console.log(checkRes) // => Left(用户名不能以数字开头密码长度必须大于6位)

const checkRes2 = checkUserInfo({ name: 'Melo', pw: '1234567' })
console.log(checkRes2) // => Right(true)

现在 checkUserInfo 函数的返回值是一个 Either(Left or Righr) 函子，具体后面就可以继续使用 fold 函数，展示校验不通过弹窗或者进行下一步的表单提交了。

关于校验参数使用 Validation 函子更合适，这里为了聚焦讲解 Applicative Functor 理念这条主干线，就不再继续引入新概念了。

PointFree风格

上面举例说明的 checkUserInfo 函数，需要 ap 两次，感觉有点繁琐(想想如果我们需要校验更多的字段呢？)，我们可以抽象出一个 point-free 风格的函数来完成上述操作：

const apply2 = (T, g, funtor1, functor2) => T(g).ap(funtor1).ap(functor2)

function checkUserInfo(user) {
    const { name, pw, phone } = user
    const returnSuccess = R.curryN(2, success);

    return apply2(Right, returnSuccess, checkName(name), checkPW(pw))
}

apply2 函数的参数特别多，尤其是需要传递 T 这个不确定的容器，用来把普通函数 g 装进盒子里。

把一个“值”(任意合法类型，当然包括函数)，装进容器中 (Box or Context) 中有一个统一的方法叫 of ，而这个过程被称为 lift ，意为提升：即把一个值提升到一个上下文中。

再回头看看前面介绍的：Box(addOne).ap(Box(2)) 和 Box(2).map(addOne) 从结果 (Box(3)) 上来看是一样。也就说执行 map 操作 (map(addOne))等同于先执行 of (Box(addOne))，然后执行 ap (ap(Box(2)))，用公式表达就是：

F(f).ap(F(x)) == F(x).map(f)

套用公式，我们可以修改简化 apply2 函数体中的 T(g).ap(funtor1) 为 funtor1.map(g) ，看下面的对比：

const apply2 = (T, g, funtor1, functor2) => T(g).ap(funtor1).ap(functor2)

const liftA2 = (g, funtor1, functor2) => funtor1.map(g).ap(functor2)

看到了上面的关键点了吗？上面的 liftA2 函数中不再耦合于 “T” 这个特定类型的盒子，这样更加的通用灵活。

按照上面的理论，可以改写 checkUserInfo 函数为：

function checkUserInfo(user) {
    const { name, pw, phone } = user
    const returnSuccess = R.curryN(2, success);

    return liftA2(returnSuccess, checkName(name), checkPW(pw))
}

现在再假设一下我们新增了需要校验的第三个字段“手机号码”，那完全可以扩展 liftA2 函数为 liftA3，liftA4 等等:

const liftA3 = (g, funtor1, functor2, functor3) => funtor1.map(g).ap(functor2).ap(functor3)
const liftA4 = (g, funtor1, functor2, functor3, functor4) => funtor1.map(g).ap(functor2).ap(functor3).ap(functor4)

刚开始可能会觉得 liftA2-3-4 看起来又丑又没必要；这种写法的意义在于：固定参数数量，一般会在函数式的 lib 中提供，不用自己手动去写这些代码。

Applicative Functor 和 Functor 的区别和联系

根据 F(f).ap(F(x)) == F(x).map(f)，我们可以得出一个结论，假如一个盒子 (Box) ，实现了 ap 方法，那么我们一定可以利用 ap 方法推导出一个 map 方法，如果拥有了 map 方法，那它就是一个 Functor ，所以我们也可以认为 Applicative 是 Functor 的拓展，比 Functor 更强大。

那么强大在何处呢？Functor 只能映射一个接收单个参数的函数(e.g., x => y)，如果我们想把接收多个参数的函数(e.g., x => y => z)应用到多个值上，则是 Applicative 的舞台了，想想 checkUserInfo 的例子。

毫无疑问，Applicative Funtor 可以 apply 多次（当然包括一次），那么如果函数只有一个参数的情况下，则可以认为 map 和 apply 是等效的，换句话说：map 相当于 apply 一次。

上面是实际应用中的对比，从抽象的数学层面来对比：

Functor: 应用一个函数到包裹的值：Box(1).map(x => x+1).
Applicative: 应用一个包裹的函数到包裹的值：Box(x => x+1).ap(Box(1))。

applicative vs functor

总结与计划

我们从纯函数与副作用的概念入手介绍了 LazyBox (惰性求值)的概念，从而引入了把函数这个“特殊的值”装进 Box 中，以及怎么 apply 这个“盒子中的函数”，然后介绍了函数柯里化与应用函子的关系(被装进盒子里的函数必须是柯里化的函数)；然后使用使用扩展后的 Either 来做表单校验，解耦合函数，最后介绍了使用 point-free 风格来编写链式调用。

计划

到目前为止，我们所讨论的问题都是同步的问题，但是在 Javascript 的世界中 90% 的代码都是异步，可以说异步才是 JavaScript 世界的主流，谁能更优雅的解决异步的问题，谁就是 JavaScript 中的大明星，从 callback ，到 Promise ，再到 async await ，那么在函数式编程中异步又该如何解决呢，下一章我们将会介绍一个重量级的概念 Monad 以及异步函数的组合。

参考资料与引用文章：

本文发布自网易云音乐大前端团队，文章未经授权禁止任何形式的转载。我们常年招收前端、iOS、Android，如果你准备换工作，又恰好喜欢云音乐，那就加入我们 grp.music-fe(at)corp.netease.com！